排序合集(上)
常见排序
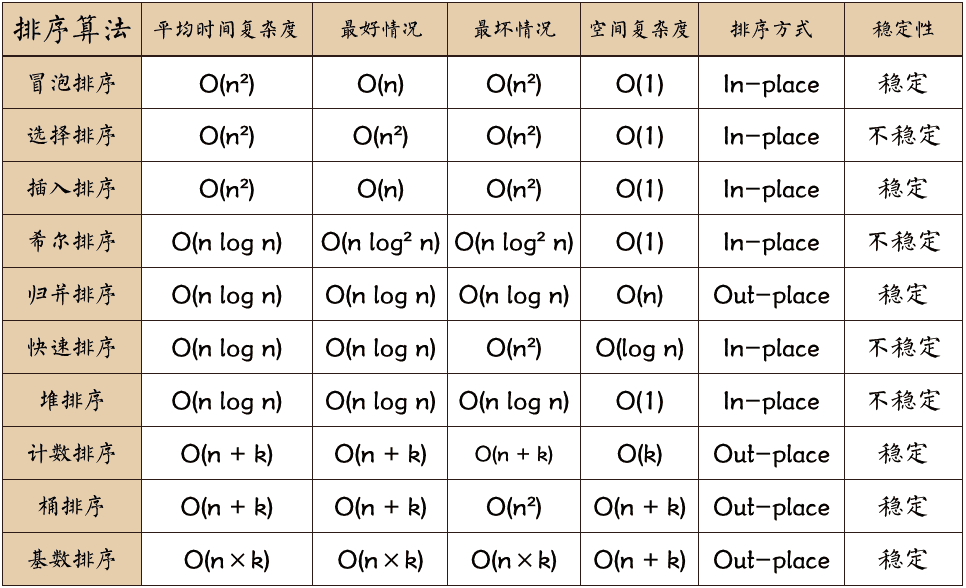
冒泡排序
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
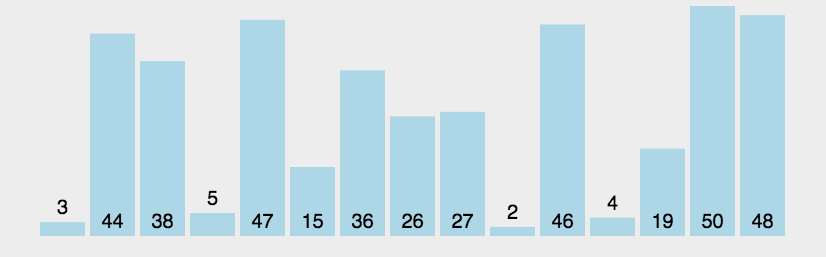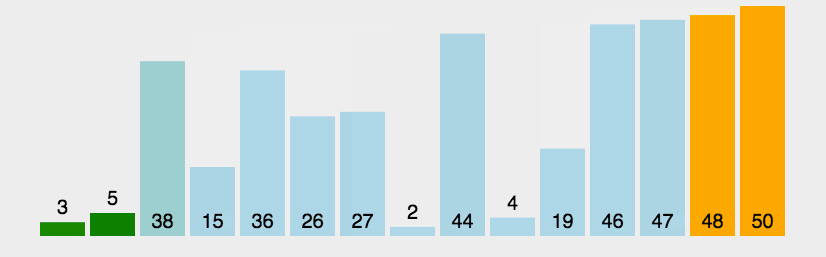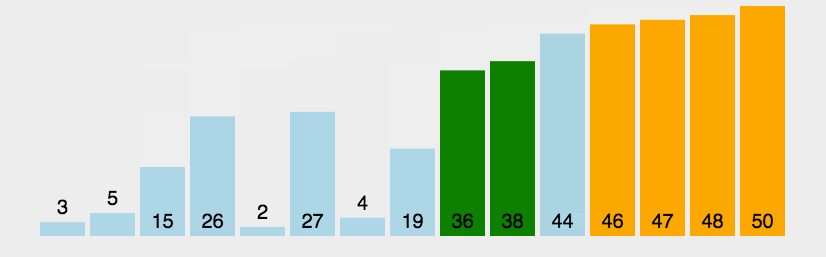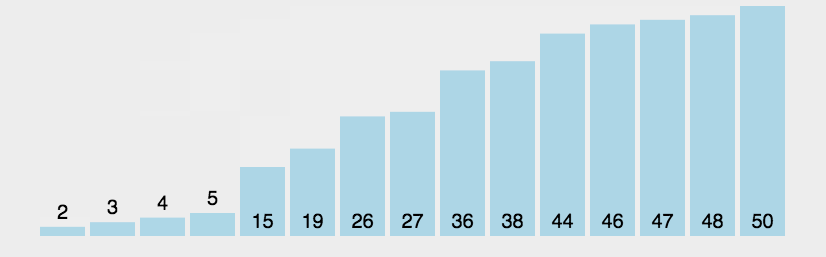
void bubbleSort(int arr[]){
for(int i = n - 1; i > 0; i--){
if_swap = false;
for(int j = 0; j < i; j++){
if(arr[j] > arr[j + 1]){
swap(arr[j + 1],arr[j]);
if_swap = true;
}
}
if(if_swap==false){
break;//如果没有发生交换,说明已经是有序序列
}
}
}
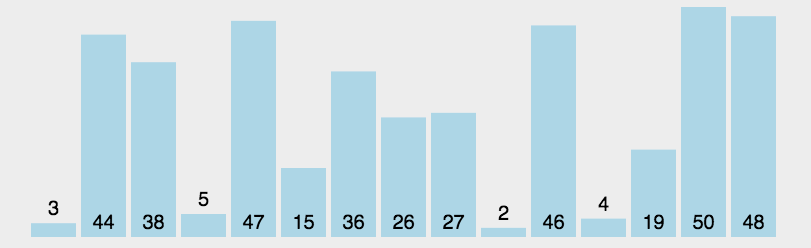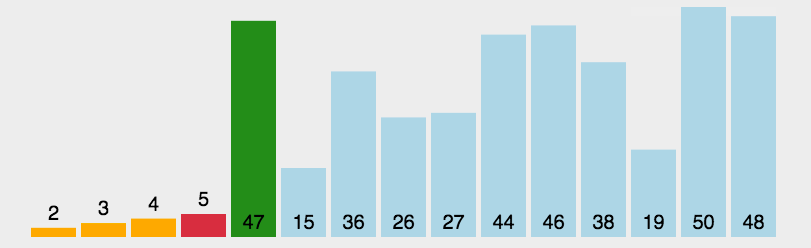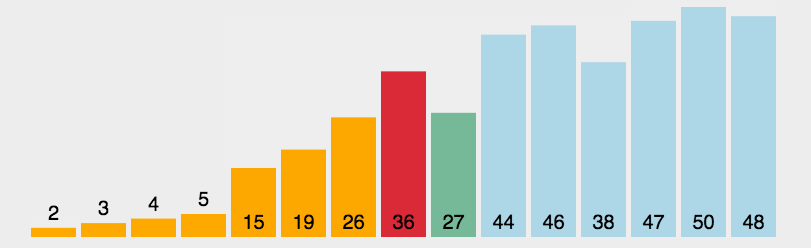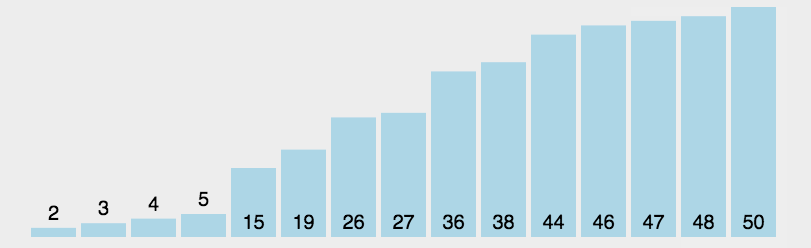
选择排序
- 在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
- 从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。
void selectSort(int arr[]){
for(int i=0;i<n-1;i++){
int minx=i;
for(int j=i+1;j<n;j++){
if(arr[minx]>arr[j]){
minx=j;
}
}
if(minx!=i)swap(arr[i],arr[minx]);
}
}
插入排序
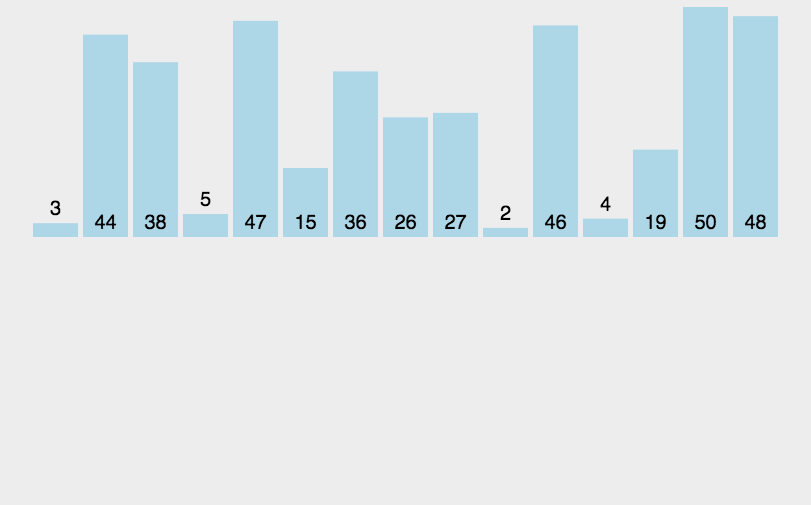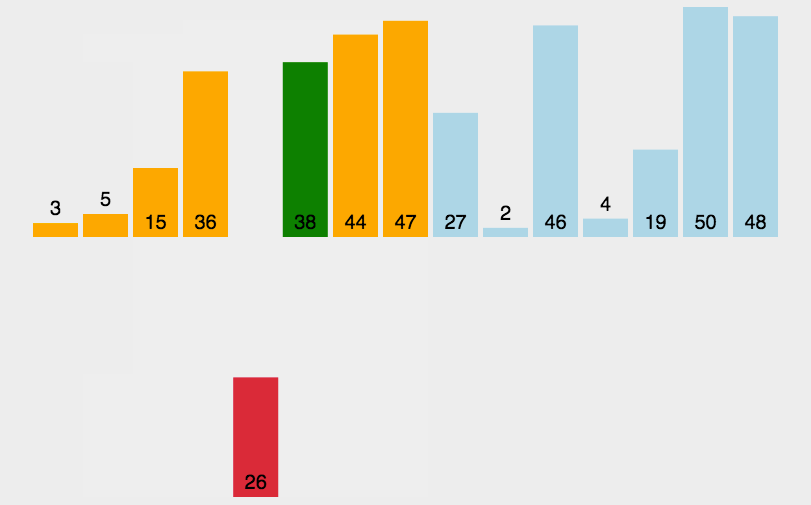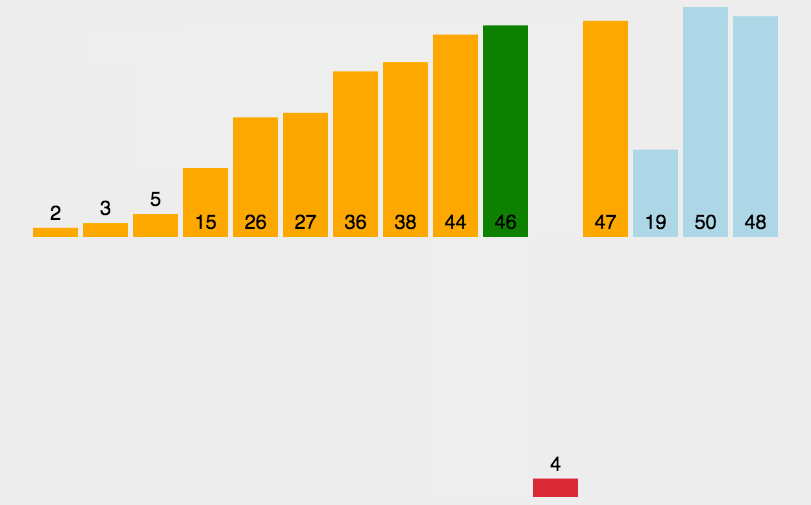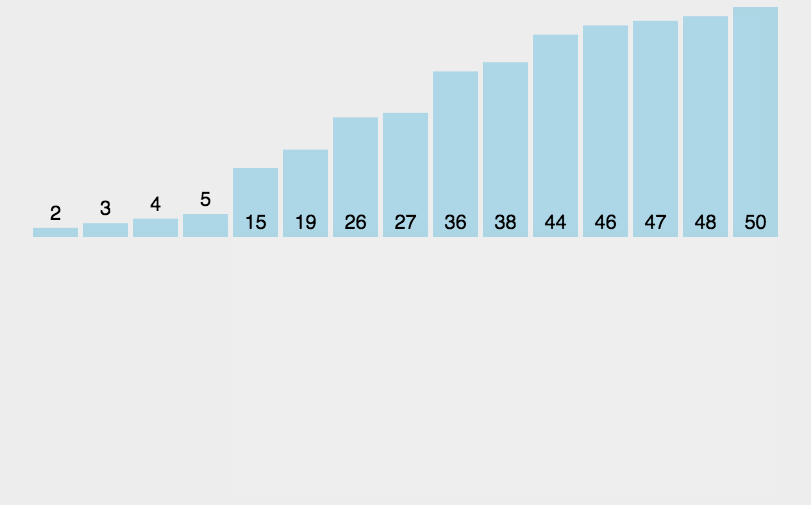
- 把待排序的数组分成已排序和未排序两部分,初始的时候把第一个元素认为是已排好序的。
- 从第二个元素开始,在已排好序的子数组中寻找到该元素合适的位置并插入该位置。
- 重复上述过程直到最后一个元素被插入有序子数组中。
void insertSort(int arr[]){
for(int i=1;i<n;i++){
int pos=i;
int value=arr[i];
while(pos>0&&arr[pos-1]>value){//向前找比自己大的最后一个位置插入
arr[pos]=arr[pos-1];
pos--;
}
arr[pos]=value;
}
}
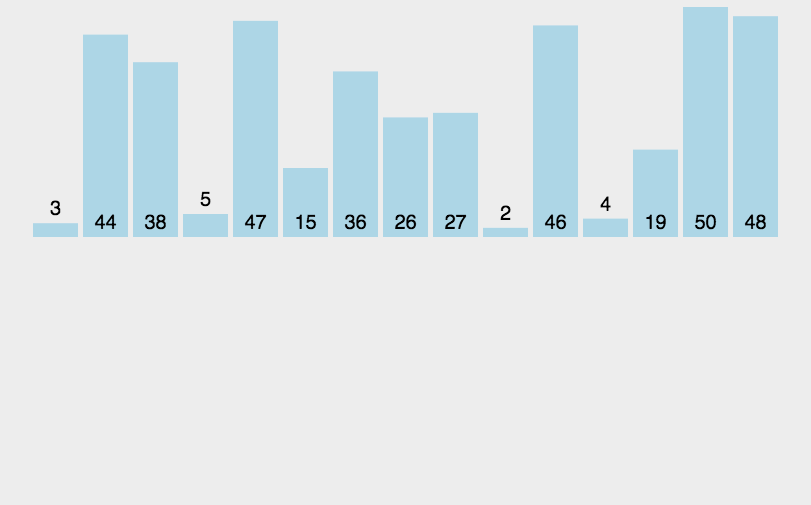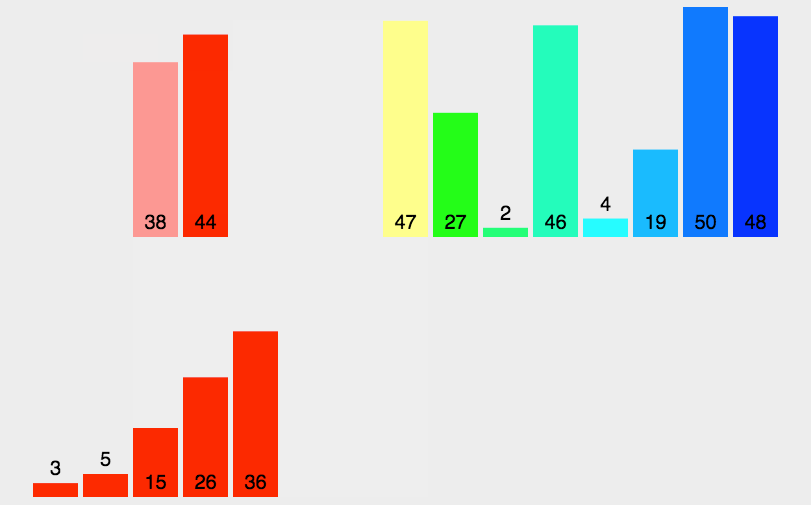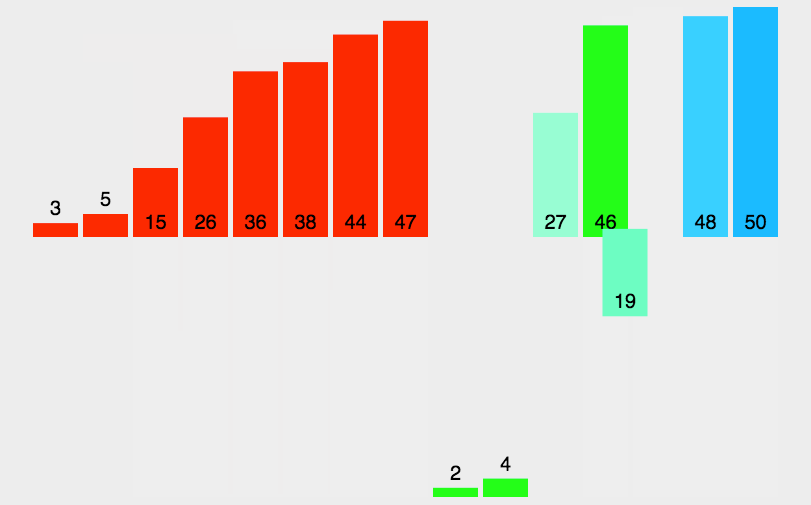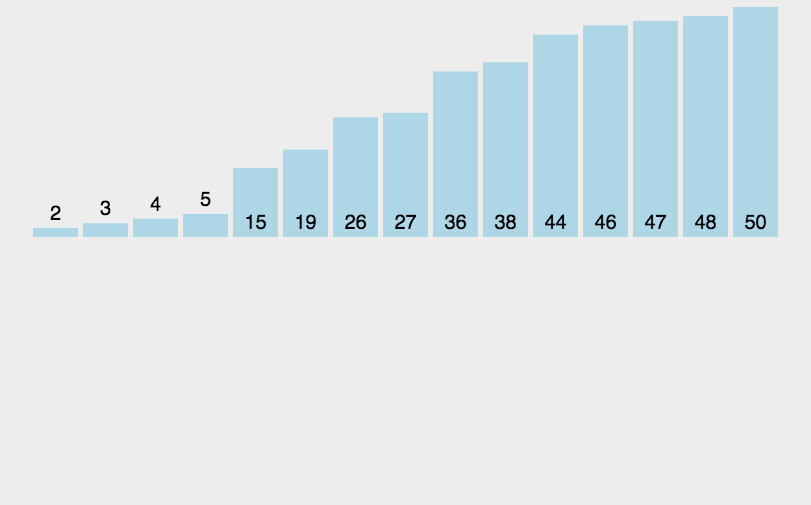
归并排序
- 先使每个子序列有序,再使子序列段间有序
- 将已有序的子序列合并,得到完全有序的序列
void mergeSort(int arr[],int l,int r){
if(l>=r)return;
int mid=(l+r)>>1;
mergeSort(arr,l,mid);
mergeSort(arr,mid+1,r);//分治思想,递归
int i=l,j=mid+1;
int temp[r-l+1],k=0;
while(i<=mid&&j<=r){//合并子序列
if(arr[i]<=arr[j])temp[k++]=arr[i++];
else temp[k++]=arr[j++];//二路归并
}
while(i<=mid)temp[k++]=arr[i++];
while(j<=r)temp[k++]=arr[j++];//剩余序列直接加上
for(int i=l,k=0;i<=r;i++,k++)arr[i]=temp[k];
}
快速排序
- 从数列中挑出一个元素,称为”基准”,
- 重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任何一边)。在这个分区结束之后,该基准就处于数列的中间位置。
- 递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。
void quickSort(int arr[],int l, int r){
if(l>=r)return;
int i=i-1,j=r+1;
int x=arr[(l+r)>>1];
while(i<j){
do{i++;}while(arr[i]<x);
do{j--;}while(arr[j]>x);//大的放前面,小的放后面
if(i<j)swap(arr[i],arr[j]);
}
quickSort(arr,l,j);
quickSort(arr,j+1,r); //分治递归
}
堆排序
堆是一种特殊的完全二叉树。
堆排序就是把最大堆堆顶的最大数取出,将剩余的堆继续调整为最大堆,再次将堆顶的最大数取出,这个过程持续到剩余数只有一个时结束。void down(int u){
int t = u;
if(2 * u <= n && arr[2 * u] < arr[t]) t = 2 * u;//有左儿子,并且左儿子比t节点的值小,更新t
if(2 * u + 1 <= n && arr[2 * u + 1] < arr[t]) t = 2 * u + 1;//有右儿子,并且右儿子比t节点的值小,更新t
if(u != t){
swap(arr[u],arr[t]);//交换节点
down(t);//递归
}
}
void heapSort(){
for(int i=n/2;i>=1;i--)down(i);//从第一个非叶节点开始,从右到左,从下到上处理每个节点
while(m--){
cout<<arr[1]<<" ";
swap(arr[1],arr[n]);
n--;//输出第一个元素,再交换到最后,再删去
down(1);//递归处理左右子节点
}
}
希尔排序
- 选择一个增量序列$t_1$,$t_2$,…,$t_k$,其中$t_i>t_j$,$t_k=1$;
- 按增量序列个数k,对序列进行 k 趟排序;
- 每趟排序,根据对应的增量$t_i$,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
void shellSort(int[] arr){
for (int delta = n /2; delta>=1; delta/=2){ //确定增量
for (int i=delta; i<n; i++){ // 进行 n-delta 次排序
for (int j=i; j>=delta && arr[j]<arr[j-delta]; j-=delta){
swap(arr[j-delta],arr[j]);//交换
}
}
}
参考文章:十大排序算法



